
 |
Eager Space | Videos by Alpha | Videos by Date | All Video Text | Support | Community | About |
|---|


https://www.nasa.gov/smallsat-institute/sst-soa/thermal-control

Lunar starship is the human lander for NASA's Artemis missions.
For the lunar starship to work requires that it be refueled in earth orbit before it journeys to the moon. It will either be refueled directly by tankers, or it will be refueled from an orbital propellant depot that is filled by tankers.
Nobody has built an orbital propellant depot like this before, and I'm seeing a lot of speculation about whether it's feasible to keep liquid oxygen and liquid methane liquid in orbit, or whether it will all just boil away.
One of my arguments has been that NASA clearly thinks SpaceX can do this or they wouldn't have given them the contract, but I thought it would be nice to have an analysis of how well an orbital depot could actually work.
Welcome to starship orbital depot analysis.
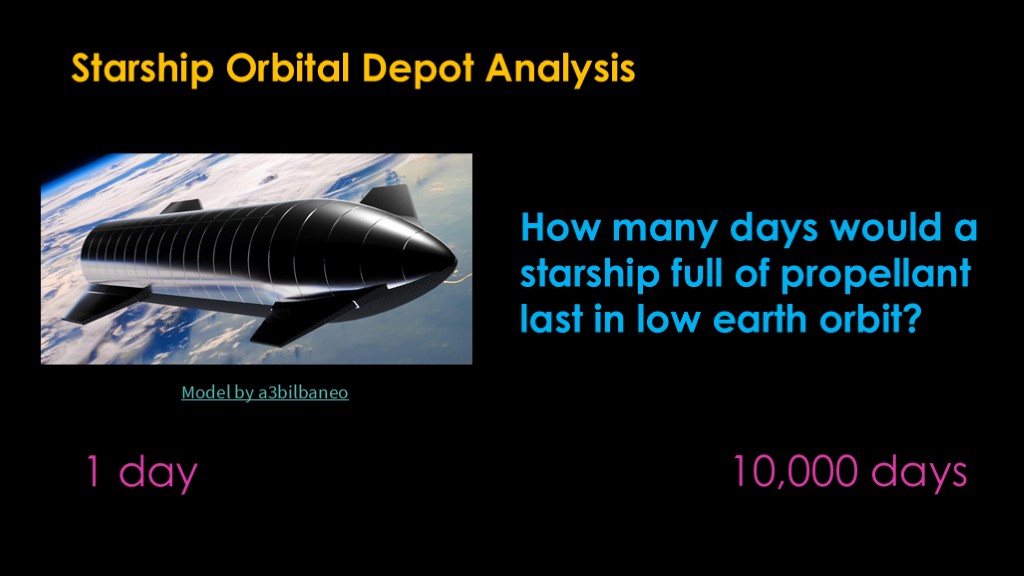
My goal is to estimate how many days the propellant in starship will last in low earth orbit before it is all vaporized.
What is your guess?
I'll give you some help. It's more than 1 day and it's less than 10,000 days.
Write down your guess, and we'll get started...
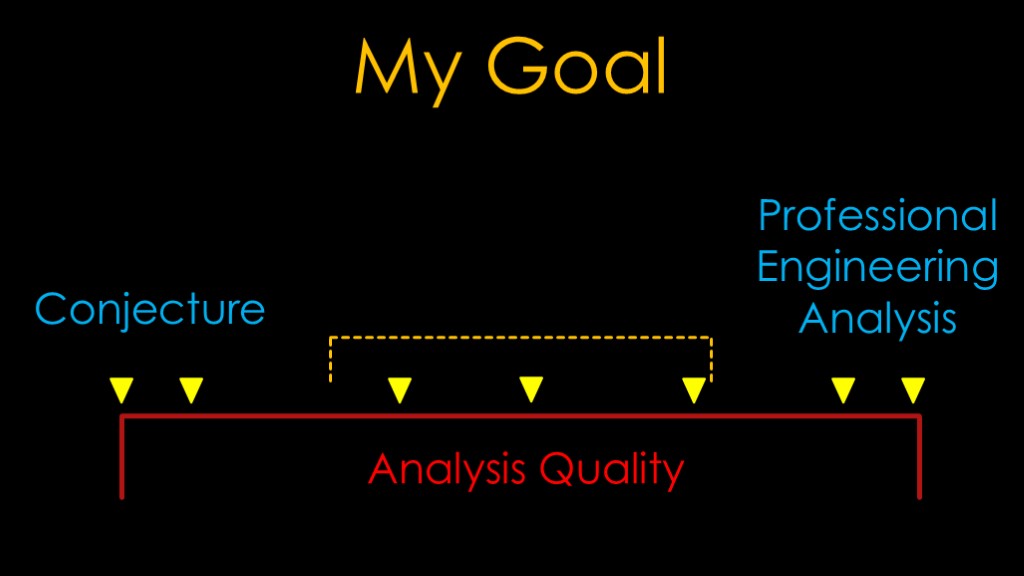
Before we get into the details, I need to explain my goal.
We can define an analysis quality scale.
On the left end we have conjecture. It might be total conjecture or it might be informed conjecture, but it's mostly just a guess.
It's fine to use conjecture in discussions, as long as you remember that it's just conjecture and there is probably better data out there.
At the other end of the scale, we have professional engineering analysis. This is what we would expect from NASA or SpaceX, work done by skilled engineers using advanced approaches and validated by other engineers. This analysis also comes at various quality levels - it could be an result that takes one engineer a few hours to create or it could be one that takes a team several months.
My goal is to be somewhere in this middle range. I'm hoping I will be near the top for most topics, but it's possible I will be lower. This particular topic seems endlessly complex and I've simplified it considerably, and some of those simplifications may overlook important concerns.

We are going to be talking about heat transfer in spacecraft - specifically about heat absorption in spacecraft.
When a spacecraft is on a planet such as a earth, we would need to consider the three ways that heat flows -
Conduction from direct contact, convection by the motion of molecules, and direct energy transfer by radiation.
In space, things are simpler - we just need to consider heat transfer by radiation.
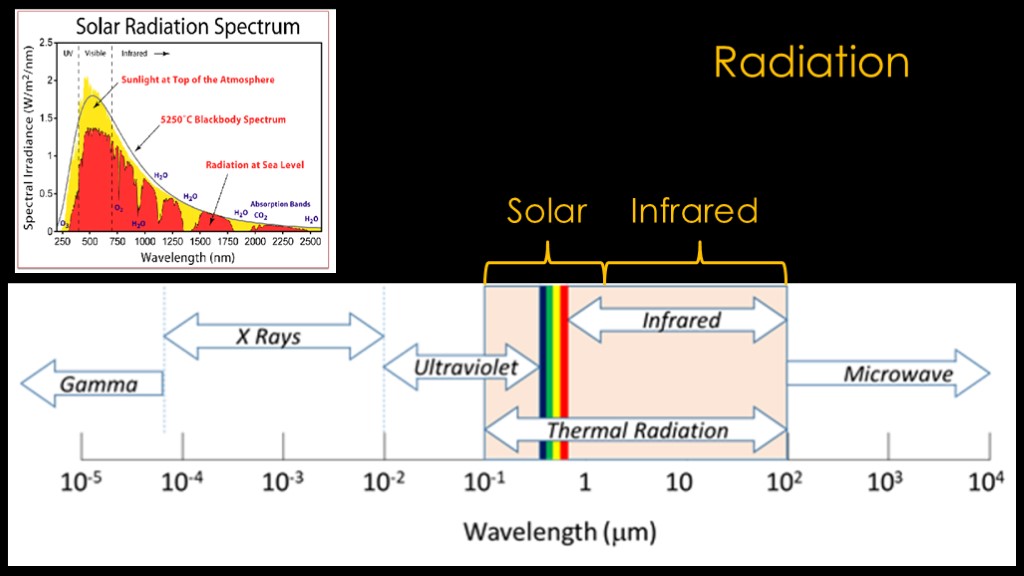
Radiation consists of many different wavelengths of light, from the very short wavelength gamma rays to the longer microwaves, and the very long radio waves that are off the slide to the right.
We are obviously concerned about heat from the sun. The surface of the sun is very hot - about 5800 Kelvin - and the radiation from very hot things is concentrated at the shorter wavelengths - ultraviolet light, visible light, and the shorter part of the infrared range. Solar radiation runs from about 0.25 micrometers on the left side and about 3 micrometers on the right side.
The remainder of the important thermal wavelengths is known as the infrared, or IR range. We will use these two ranges as part of our analysis.
https://www.researchgate.net/figure/Solar-Radiation-Spectrum-Solar-radiation-is-the-radiant-energy-emitted-by-the-Sun-Fig-1_fig2_287748270
https://www.nasa.gov/smallsat-institute/sst-soa/thermal-control#_Toc120613720

The sun is putting out radiation that is hitting our spacecraft. You already know something important about sunlight. If you are wearing a black shirt in the sun you will get much hotter than if you wear a white shirt, because the black shirt is better at absorbing the energy and the white shirt is better at reflecting the energy.
In engineering terms, the amount of solar radiation that is absorbed is known as absorptability, often denoted using the lowercase Greek letter alpha. A surface that is great at reflecting solar radiation will have a low value such as 0.1, and a surface great at absorbing solar radiation will have a high value such as 0.9.
Note that it's not just about how light or dark a material appears to humans, as that is only about visible light, and a surface that reflects visible light well may not reflect ultraviolet or infrared well.

The intensity of the sun at the earth is 1367 watts per square meter. If our absorptability is 0.4, that means each square meter of the spacecraft will be absorbing 547 watts.
That added heat will cause the spacecraft to heat up.
We know that spacecraft don't just heat up and melt, so there must be something else going on. That something is the spacecraft emitting heat back out into space as infrared radiation. When the spacecraft is emitting the same amount of total heat as the sun is adding, it will be at a stable temperature.
Can we figure out that temperature?

The answer is yes, but it's a little complicated...
The first thing we need to know is that there is a analog to absorptability known as emissivity, usually denoted with the lower case Greek letter epsilon. Emissivity also ranges from 0 to 1, and it tells us how good a surface is at emitting or absorbing infrared light.
If we know the emissivity of our spacecraft is 0.6, that means we would need enough heat to be capable of emitting 912 watts per meter to be actually emitting 547 watts per meter.
Now that we know that number, we can use an equation known as "the Stefan-boltzman law", and it will tell us that the surface of the spacecraft will be 356 kelvin, which is 83 degrees Celsius or 181 Fahrenheit. Getting pretty close to boiling.
The study of this sort of situation is known as thermodynamics, or "thermo" if you want to hang out with the cool kids.
This particular analysis is significantly wrong. The sun only heats one side of the spacecraft, but the spacecraft emits infrared radiation from all sides and those two sides are also different temperatures so they emit different amounts of power. That's the sort of complication that makes thermodynamics so much fun.

In this video, you can safely ignore any slide with the "details" label in the corner as this material will not be on the test, but some viewers do want to know how the calculations are done.
For the heat input calculation, we take the total solar power and multiply by the absorptability constant to get the net input power. I didn't find any information about whether the derived value is based on the solar spectrum, but I can tell you that there are different ways to get that value with different equipment and it's not surprisingly more complex than you might think.
The temperature calculations use the Stefan-Boltzman law, which says that the power in watts is equal to the boltzman constant multiplied by the emissivity constant, the area in square meters, and the temperature in kelvin raised to the fourth power.
That fourth power in the equation means that the power output goes *way* up as the temperature increases. It's why the sun provides so much energy to the solar system.
BTW, there is nobody named "Stefan Boltzman" - it is the work of Ludwig Boltzman and Josef Stefan.
In our case we know the power that is going out needs to be the same as the power coming in, so we refactor the equation to solve for T and plug in the values for our case. Area is always 1 because we are looking at the power coming in and going out for the same square meter.
That gives us a temperature of 356 kelvin.

Now that we know a little about analysis, we can look at the orbital propellant depot.
We'll start with a stock starship in orbit around the earth. It has a tank of liquid oxygen at 90 kelvin and a tank of liquid methane at 112 kelvin.
Note that I've drawn cylindrical tanks rather than the actual shape of starship tanks. You can redo the analysis with actual tank shapes for extra credit.

There are three sources of heat gain for our propellant depot.
The sun provides the usual 1367 watts per square meter, but in LEO we're only in the sun for about half of the orbit, so the average heat gain is half that, or 684 watts per square meter. Multiply that by 0.42 - the absorptability of stainless steel - and we get 287 watts per square meter.
The second source of energy is the sunlight reflected off of the earth. We take the energy delivered by the sun and multiply it by the albedo of the earth - the proportion of light that is reflected back to space which is about 0.16. That gives us 219 watts per square meter.
Like the sun, we only get reflected light during half the orbit, which drops us down to 109 watts per square meter. Multiply by the absorptablity, and we get a net energy gain of 46 watts per square meter. We could also just have taken the net power of 287 watts per square meter and multiplied it by the albedo.
That takes us to the third component of heat gain - the infrared energy coming from the earth because the earth is hot. NASA estimates this at 240 watts per square meter. The earth is radiating on both the sun side and the dark side. Because this is IR radiation, we use the emissivity to calculate the effect of this - and we end up with 26 watts per square meter.
There are two additional sources to consider. The first is the infrared emitted by the propellant tank. The liquid methane is at 112 K, and the lox is at 90 k - that's cold enough that it's less than 1 watt per meter squared.
The second is heating from the background 3 kelvin cosmic radiation. It's less than a millionth of a watt per square meter. We will safely ignore both of these.
Based on how much heat the tanks are getting, we can figure out how much heat gain there is each day, how much propellant it vaporizes each day, and how long until the tanks are empty.
Here's a chance to see how good your guess was...
The LOX tank will last for 55 days, and the liquid methane tank will last for 50 days.
Those are bigger numbers than I expected - if you launched a tanker a day, I don't think the boiloff would be significant.
But we can do better.

Time for some more math.
To go from the amount of heat per square meter to the total heat, we need to figure out how much of the tank is exposed to that heat.
To make things simple, I'm assuming radiation hitting the side of a cylinder is equivalent to hitting a flat surface with the same diameter. This ignores the fact that absorptability depends on the angle that the sunlight hits - rays hitting near the edge are more likely to be reflected. I'm making the same assumption for reflected light from the earth. I'm also assuming that the light is hitting directly from the side, not obliquely. There are models that do not assume that, and they will likely give more accurate results.
The absorbing area is therefore just 9 meters multiplied by the height of the tank, or 112.5 square meters for the liquid oxygen tank.
To figure out the lifetime, we start by adding the three heat fluxes from sunlight, reflected sunlight, and earth IR to get 359 watts per square meter. Multiply it by 112.5 square meters and we end up with a bit more than 40 kilowatts of power.
That seems like a lot.
1 watt is equal to 1 joule per second, so that's 40.4 kilojoules per second.
Multiply that by the 86,400 seconds in a day, and we get nearly 3.5 million kilojoules per day.
The amount of liquid oxygen that much energy can vaporize is determined by taking the energy and dividing it by the heat of vaporization for liquid oxygen, which is 214 kilojoules per kilogram, giving us 16,300 kilograms vaporized per day.
The liquid oxygen tank holds 906,000 kilograms, so that means that it will take 55 days to evaporate all of the liquid oxygen.
The liquid methane lifetime is figured out the same way, using the size and capacity of that tank.
That's our baseline, the performance we get from a standard starship.

The obvious thing to do is to look for a better material than stainless steel. There are lots of coatings made for spacecraft to reduce thermal gain. I've chosen a coating known as AZW/LA-II from AZ technology.
This coating has an absorptability of 0.09. Looking at our solar energy absorption, that reduces it by 78%, down to 62 watts per square meter. We see a similar reduction on the light from the earth, down to 10 watts per meter.
This is looking great.
We now look at the earth infrared component. The emissivity went from 0.11 to 0.91, which bumps the IR heat gain all the way up to 218 watts per meter. The bulk of the heat gain is now from earth IR. Our lifetimes go up to 71 and 67 days, but that's only a small change.
This coating is designed for satellites that are warm enough to radiate quite a bit of infrared, but our LOX tank is cold enough that it will never radiate much heat, so a higher emissivity is worse for us.
Earth IR turns out to be a significant issue for earth-orbiting satellites. We want a high emissivity to radiate power back to space and stay cool, but that high emissivity means we absorb a lot of the earth IR and that warms us up.
For our scenario, a coating with a lower emissivity might be a better choice.
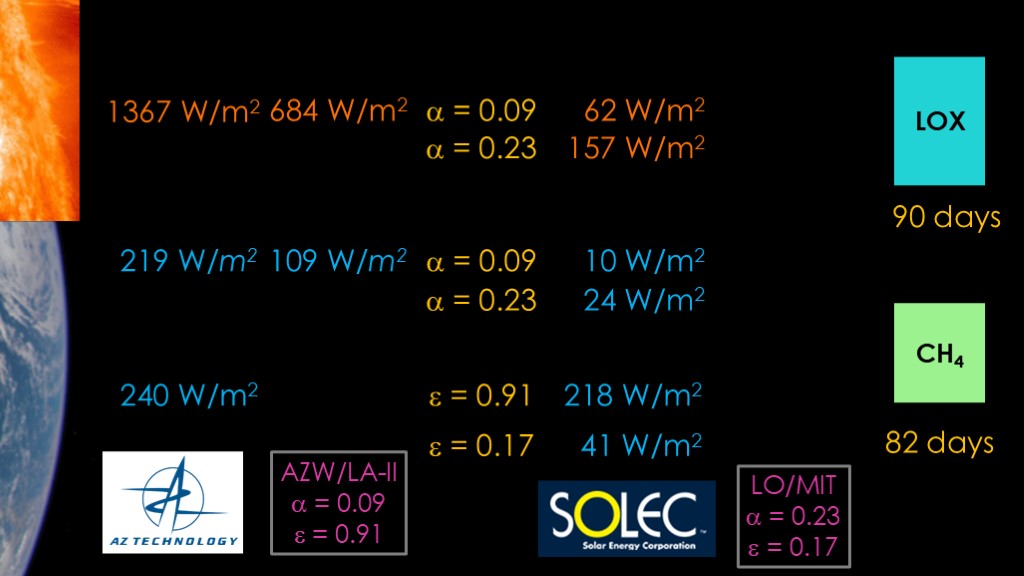
We find that not in the space industry, but in the solar industry.
Solec makes a coating they call LO/MIT, with an absorptability of 0.23 and an emissivity of 0.17. The higher absorptability pushes the solar and reflected gain back up by a total of 109 watts, but the IR absorption is 177 watts lower, so our overall reduction is 68 watts,
Our lifetime goes up to 90 days and 82 days.
There has been a lot of research on coatings and there are very likely coatings that are better for our scenario, but I think the current lifetimes make HLS scenarios quite possible.
Are there other techniques we could use?
http://www.solarmirror.com/fom/fom-serve/cache/43.html
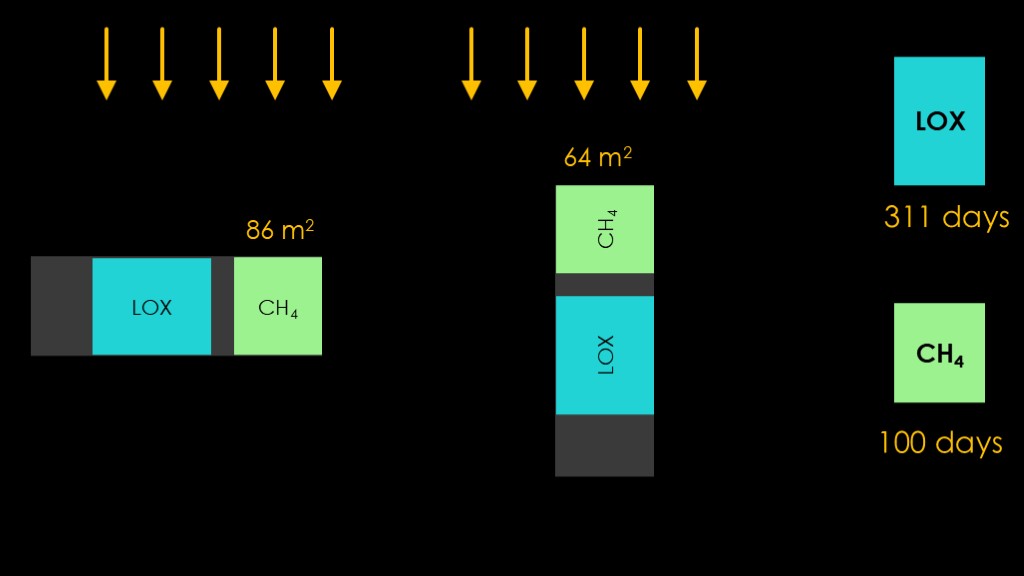
We have been assuming that our tanks are sideways to the sun.
But what if we rotate the depot so the nose is facing the sun and keep it that way? That will reduce the area of the liquid methane tank from 86 square meters down to 64 square meters and push that lifetime up to 100 days.
This orientation totally shields the LOX tank from solar radiation, which means it only heats up from reflected sunlight and infrared from the earth, for a 311 day lifespan.

We now have a bit of a coating mismatch.
We have LO/MIT on the sides where it is great dealing with the earth IR and decent at dealing with reflected sunshine, but we also have it on the front that is exposed to the sun, where it's pretty bad at dealing with solar radiation.
If replace LO/MIT with AZW/LA-II on the nose, we reduce the solar gain considerably, bumping the liquid methane tank lifetime from 100 days to 167 days.

There's one more trick to play. Instead of having the liquid methane tank face the sun, we add a flat nose spaced 1 meter from the top of the liquid methane tank, with space in between.
With the AZW coating, it will absorb 123 watts per square meter of heat, and it will heat up until it emits that much energy.
Some of that energy will be radiated out to space and some will be radiated inside towards the top of the liquid methane tank.
The amounts will depend on the relative emissivity of the two surfaces. The outside one is 0.91 and the inside 0.11, so most of the energy goes towards the outside. It turns out to be 110 watts per meter squared outside and only 13 watts per meter squared for the inside.
That's a big difference in the solar gain to the liquid methane tank. It's low enough to get rid of the majority of the heat gain from the sun, and push the liquid methane tank lifetime out to 246 days.
At this point, the majority of the heat gain for that tank is coming from the earth. (do a chart for all of these to show the relative contributions?)
(math: 123 = T4 1 + T4 2 )
123 = T4 (1 + 2)
1 = 110W, 2 = 13W
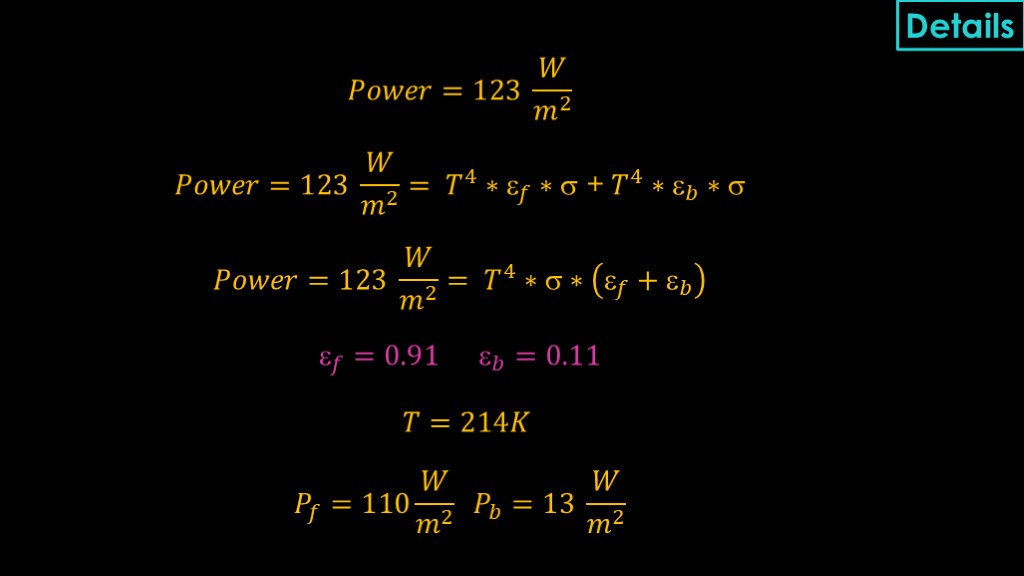
Somebody is going to want the math, so here's what I came up with...
The power being absorbed is 123 watts per square meter.
That will be radiated to the front based on the emissivity to the front, and to the rear based on the emissivity to the back. We can refactor our equation and find that the power is the temperature raised to the fourth power times the boltzman constant times the sum of the front and back emissivity.
We know the AZW/LA-II is 0.91, and the raw stainless steel is 0.11. Solving for T, we get a temperature of 214 kelvin.
We can then figure out the two components, with 110 watts per square meter coming off the front and only 13 watts per square meter coming off the back and hitting the liquid methane tank.

What are our conclusions?
Based on the model, standard starship is probably good enough for HLS with a decent refueling cadence. Using simple coatings and/or a specific orientation makes things a lot better.
There are two big caveats.
This model has a lot of assumptions built into it, some of which might be problematic.
Second, heat models are hard, and there might be mistakes in this one. This information is presented for informational use only, and orbital propellant depot owners should consult a skilled professional whenever heat is involved.

And that's my analysis of starship as an orbital depot.
Some of you have probably noticed there's another heat analysis for this project.
Lunar starship will need to sit on the lunar surface for at least a week and retain enough propellant to get back into lunar orbit.
As soon as my brain has recovered a bit, it will be time to use the same principles and analyze what happens to the liquid oxygen and liquid methane with lunar starship sitting on the lunar surface. You'll probably want to subscribe so you don't miss that video, and you should also start thinking what your guess is for the lifetime in days...

If you enjoyed this video, please fact check the Wikipedia article on the Stefan Boltzmann law...